Numerot ympäröivät meitä kaikkialla – kellotauluissa, askelmäärissä ja tiliotteissa. Ne tuntuvat ajattomilta, mutta näin ei tietenkään ole. Jokainen numerojärjestelmä, laskutapa, merkki ja symboli on keksitty ja niitä on kehitetty tuhansien vuosien ajan.
Ihmiset ovat laskeneet paljon ennen kirjoitettuja järjestelmiä. Jo kymmeniä tuhansia vuosia sitten lukumääriä seurattiin tekemällä luunpaloihin lovia tai asettelemalla keppejä pinoihin. Vähitellen syntyi järjestelmiä, joiden symboleilla voitiin esittää yhä suurempia ja tarkempia lukuja.
Mielenkiintoista tästä tekee se, että eri sivilisaatiot ratkaisivat matemaattisia ongelmia eri tavoilla mutta samoihin tarpeisiin: peltojen mittaamiseen, verojen keräämiseen ja kauppatavaran jakamiseen. Egyptin hieroglyfit, Babylonian seksagesimaalit, Kiinan laskentapuikot ja Kreikan abstraktit todistukset ovat kaikki jättäneet jälkensä moderniin matematiikkaan.
Egyptiläiset hieroglyfit
Länsimaissa ja ympäri maailmaa käytetään desimaalijärjestelmää, joka nojaa paikkamerkintään: luvun arvo riippuu käytettävien numeromerkkien arvoista ja niiden keskinäisestä järjestyksestä. Luvussa 1000 on siis oikealta vasemmalle ykköset, kymmenet, sadat ja tuhannet.
Muinais-Egyptissä oli sen sijaan käytössä additiivinen merkintä, jossa merkkien arvot lasketaan keskenään yhteen. Jokaisella kymmenen potenssilla oli oma symbolinsa, ja numeroita muodostettiin liittämällä niitä toisiinsa:
| Luku | Symboli | Kuvaus |
|---|---|---|
| 1 | 𓏺 | Pystysuora viiva |
| 10 | 𓎆 | Käänteinen u-kirjain |
| 100 | 𓍢 | Kierretty köysi |
| 1 000 | 𓆼 | Lootuskukka |
| 10 000 | 𓂭 | Osoittava sormi |
| 100 000 | 𓆐 | Sammakko / nuijapää |
| 1 000 000 | 𓁨 | Heh-jumala |
Jos kirjuri halusi kirjoittaa luvun 276, hän piirsi kaksi kierrettyä köyttä (2 x 100), seitsemän käänteistä u-kirjainta (7 x 10) ja kuusi suoraa viivaa (6 x 1). Mitä suurempi luku, sitä työläämpi se oli kirjoittaa (46 237):
- neljä osoittavaa sormea (4 × 10 000)
- kuusi lootuskukkaa (6 × 1 000)
- kaksi köyttä (2 × 100)
- kolme käänteistä u-kirjainta (3 × 10)
- seitsemän viivaa (7 × 1)
Vaikka järjestelmä oli työläs, se oli selkeä ja riittävän käytännöllinen: sen avulla voitiin mitata peltoja, kirjata veroja ja jakaa palkkiot tasan. Suurten lukujen kömpelyys selittää kuitenkin osaltaan, miksi egyptiläinen matematiikka ei edennyt abstraktin teorian puolelle.
Babylonialaiset seksagesimaalit
Jos Egyptistä suuntasi itään, saapui Mesopotamiaan eli Kaksoisvirranmaahan, joka tunnetaan tätä nykyä sivistyksen kehtona. Siellä babylonialaiset kehittivät (sumerilaisten perinteiden pohjalta) uudenlaisen paikkalukujärjestelmän.
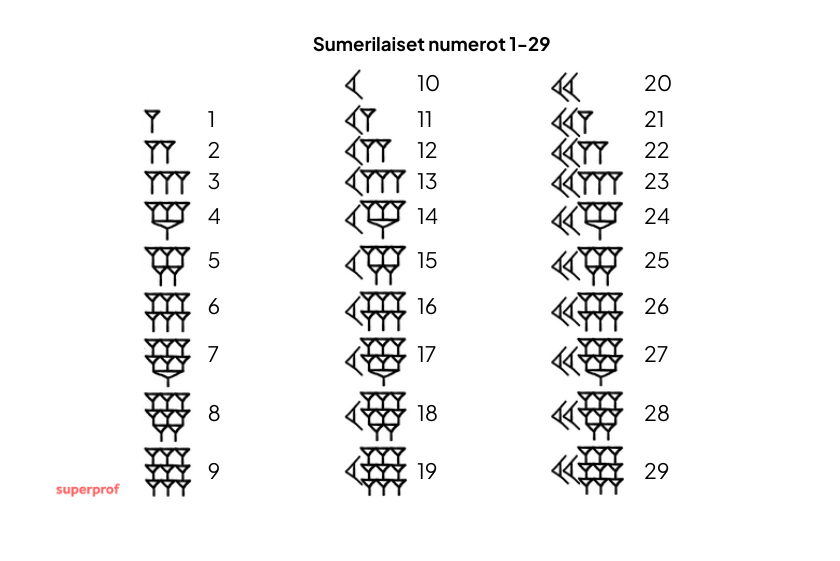
Järjestelmä hyödynsi sumerien nuolenpääkirjoitusta, jossa yksi kiila merkitsi ykköstä (𒁹) ja kulmakiila kymppiä (𒌋). Järjestelmän kantaluku ei kuitenkaan ollut meille tuttu 10 vaan 60, ja numerot 1–59 muodostettiin tavallisia ja kulmakiiloja yhdistämällä:
- 23 merkittiin 𒌋𒌋𒁹𒁹𒁹 (10 + 10 + 1 + 1 +1)
- 125 merkittiin 𒁹𒁹␣𒁹𒁹𒁹𒁹𒁹 (2 x 60 + 5 x 1)
Paikkajärjestelmä oli mullistuksellinen, sillä se helpotti suurten lukujen ja murtolukujen käsittelyä. Kantaluvuksi valikoitui 60 todennäköisesti siksi, että se on jaettavissa monella eri luvulla: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.
Mesopotamiaa kutsutaan usein sivistyksen kehdoksi. Sinne nousivat ensimmäiset suuret kaupungit ja siellä syntyivät kirjoitustaito (kiilakirjoitus) sekä varhaiset lakikokoelmat, kuten Hammurabin lait. Hedelmällinen jokilaakso mahdollisti maanviljelyn ja kastelun, mikä johti väestön kasvuun ja erikoistuneisiin ammatteihin.
Vaikka järjestelmällä oli omat rajoituksensa, se taipui mutkikkaisiinkin laskuihin. Savitauluilta on löydetty toisen asteen yhtälöiden ratkaisuja, Pythagoraan kolmikoita ja tähtitieteellisiä taulukoita, jotka osoittavat babylonialaisten ottaneen ensimmäisiä askeleita kohti teoreettista matematiikkaa.
Kiinalainen puikkolaskenta
Kiinalaiset kehittivät varhain loogisen ja johdonmukaisen desimaalijärjestelmän, jonka kantaluku oli 10: kymmenessä on kymmenen ykköstä (101), sadassa kymmenen kymmentä (102), tuhannessa kymmenen sataa (103) jne.
Järjestelmässä oli omat merkkinsä numeroille 1–9 (一, 二, 三 jne.) ja kymmenen potensseille:
- 十 (shí) = 10
- 百 (bǎi) = 100
- 千 (qiān) = 1 000
- 万 (wàn) = 10 000
- 亿 (yì) = 100 000 000
Numeroita muodostettiin kahden yksinkertaisen säännön avulla. Jos pienempi luku tuli suuremman jälkeen, ne laskettiin yhteen (百十三 = 100 + 10 + 3 = 113). Jos taas pienempi luku tuli ensin, luvut kerrottiin (三百 = 3 × 100 = 300).
Kirjoitetun järjestelmän rinnalle syntyi puikkolaskenta, jossa käytettiin apuna bambu- tai luupuikkoja. Luvut 1–4 merkittiin pystypuikoilla (|, ||, |||, ||||), luku 5 vaakapuikolla (—) ja luvut 6–9 niiden yhdistelmillä (—| = 6, —|| = 7, … —|||| = 9).
Puikkoja aseteltiin laskentapöydän sarakkeisiin, jotka vastasivat ykkösiä, kymmeniä, satoja ja tuhansia. Jotta viereiset sarakkeet eivät menisi sekaisin, ykköset ja sadat merkittiin pystypuikoilla, kymmenet ja tuhannet vaakapuikoilla.
Puikoilla pystyttiin laskemaan suuria kerto- ja jakolaskuja, murtolukuja ja jopa negatiivisia lukuja. Kirjallisten merkkien ja puikkolaskennan yhdistelmä teki kiinalaisesta matematiikasta käytännönläheistä ja tehokasta.
Kreikkalainen teoria
Antiikin kreikkalaisilla oli käytössä kaksi numerojärjestelmää: 1) ensin roomalaisia numeroita muistuttava attikalainen järjestelmä ja myöhemmin joonialainen, jossa käytettiin aakkosia ykkösille, kymmenille ja sadoille:
| Luku | Symboli | Luku | Symboli |
|---|---|---|---|
| 1 | α (alpha) | 10 | ι (iota) |
| 2 | β (beta) | 20 | κ (kappa) |
| 3 | γ (gamma) | 30 | λ (lambda) |
| 4 | δ (delta) | 40 | μ (mu) |
| 5 | ε (epsilon) | 50 | ν (nu) |
| 6 | ϛ (stigma) | 60 | ξ (xi) |
| 7 | ζ (zeta) | 70 | ο (omicron) |
| 8 | η (eta) | 80 | π (pi) |
| 9 | θ (theta) | 90 | Ϟ (koppa) |
| 100 | ρ (rho) | 900 | Ϡ (sampi) |
Muut luvut saatiin kirjainmerkkejä yhdistelemällä:
- β (beeta = 2) + ι (ioota = 10) = ιβ (12)
- δ (delta = 4) + μ (myy = 40) = μδ (44)
- ϛ (stigma = 6) + ρ (rho = 100) = ρϛ (106)
Antiikin kreikkalaisia ei kuitenkaan muisteta heidän tavastaan kirjoittaa numeroita vaan siitä, miten he ajattelivat matematiikkaa. He halusivat selvittää, miksi asiat toimivat niin kuin toimivat, ja kaiken keskelle nousi matematiikka älyllisenä harrastuksena.
Kreikkalaiset rakensivat matematiikasta loogisen kokonaisuuden, joka etenee perusolettamuksista määritelmiin ja teoreemoihin. Näin matematiikasta kasvoi tieteellinen järjestelmä, joka oli johdonmukainen ja toistettavissa.
Matematiikan avulla jäsenneltiin myös maailmaa: Pythagoraan mukaan todellisuus rakentuu numeroista ja toistuvista sykleistä, ja Platonille matematiikka toimi porttina ikuisiin totuuksiin. Uusi lähestymistapa loi perustan länsimaiselle tieteelle.
Matematiikka porttina historiaan
Matematiikka keskittyy numeroihin, mutta sen järjestelmät kuvaavat aina myös kulttuureita, yhteisöjä ja niiden arkea. Varhaisimmat järjestelmät keskittyivät käytäntöön:
- Egyptiläisillä numeroilla laskettiin pinta-aloja, kirjattiin veroja ja jaettiin palkkioita tasan.
- Babylonialaisten 60-järjestelmällä kartoitettiin aikaa ja taivaankappaleita.
- Kiinalaisten puikkolaskenta sopi niin kauppiaiden, virkamiesten kuin tutkijoiden tarpeisiin.
Kaikki näistä kehittyivät ratkomaan arjen tarpeita. Suunta muuttui kreikkalaisten myötä: kun arjen tarpeet oli täytetty, matematiikasta tuli ajattelun työkalu. Se kehittyi laskentajärjestelmästä järkeilyn, todistuksen ja filosofian raameiksi.
Yllä esiteltyjen järjestelmien perintö elää yhä. Egyptiläiset hieroglyfit muistuttavat, että kielet ja numerot ovat kehittyneet rinta rinnan. 60-järjestelmä näkyy tuntien (60 minuuttia) ja minuuttien rakenteessa (60 sekuntia). Kreikkalaisten logiikan korostus pönkittää modernia matematiikkaa ja tiedettä.
Numerot eivät siis ole pelkkiä symboleja, vaan niiden taustalta avautuu kymmeniä läpimurtoja ja kehitysaskelia, filosofisia aatteita ja käytännön työkaluja, joiden avulla ihmiset mittaavat ja jäsentävät maailmaa.
Piditkö tästä artikkelista? Jätä arvostelu!
Ladataan...
