Muinaisesta Egyptistä tulee mieleen pyramidit, sfinksit, kiveen kaiverretut hieroglyfit ja muuan Sinuhe, jotka kaikki liittyvät tavalla tai toisella matematiikkaan. Ilman sitä ei olisi pyramideja, kastelujärjestelmiä tai byrokratian ratasta, joka pyöritti Niilin laaksoa tuhansien vuosien ajan.
Egyptiläisille matematiikka ei ollut abstrakti tiede vaan selviytymisen ja valtiotaidon väline. He ratkoivat sillä ongelmia, kuten maanmittausta, verotusta ja rakenteiden kestävyyttä. Käytännön tarpeista syntyi rikas ja luova kymmenjärjestelmä, joka vaikutti moniin myöhempiin sivilisaatioihin.
Mihin matematiikkaa tarvittiin?
Muinais-Egypti rakentui Niilin ympärille. Vuosittain joki tulvi ympäröiville pelloille ja jätti vetäytyessään jälkeensä hedelmällisen maaperän. Kierto toi vaurautta mutta myös päänvaivaa: kun rajamerkit katosivat, riidat viljelysmaista lisääntyivät ja maanmittaajat joutuivat töihin.
Maanviljelys on vain yksi esimerkki. Muinais-Egypti oli keskitetty valtio, jolla oli
- mutkikas hallinto veroineen, väestönlaskentoineen ja kauppakirjoineen
- monumentaalisia rakennelmia, kuten pyramideja, temppeleitä ja obeliskeja
- insinööriprojekteja, kuten kanavia, varastoja, patoja ja tulvasuojia
- kauppaverkosto Nubiaan, Levantiin ja muualle Välimeren alueelle.
Nämä kaikki perustuivat matematiikkaan, joka oli juurtunut syvälle käytännön haasteisiin. Käytännön tarpeiden ratkaisemiseksi egyptiläiset kehittivät oman lukujärjestelmänsä.
Egyptiläiset numerot
Meille tuttu desimaalijärjestelmä nojaa paikkamerkintään: luvun arvo riippuu käytettävien numeromerkkien arvoista ja niiden keskinäisestä järjestyksestä. Luvussa 1000 on siis oikealta vasemmalle ensin ykköset, kymmenet, sadat ja lopulta tuhannet.
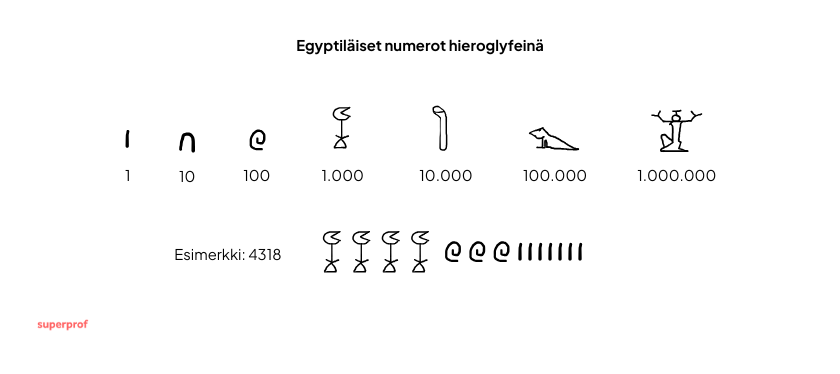
Muinais-Egyptissä käytettiin sen sijaan additiivista merkintää: luvun arvo ilmaistaan ryhmällä merkkejä, joiden arvot lasketaan yhteen. Järjestelmä nojasi egyptiläisten kirjoitusjärjestelmään eri hieroglyfeihin, joista seuraavilla merkittiin kymmenen potensseja:
| Luku | Symboli | Kuvaus |
|---|---|---|
| 1 | 𓏺 | Pystysuora viiva |
| 10 | 𓎆 | Käänteinen u-kirjain |
| 100 | 𓍢 | Kierretty köysi |
| 1 000 | 𓆼 | Lootuskukka |
| 10 000 | 𓂭 | Osoittava sormi |
| 100 000 | 𓆐 | Sammakko / nuijapää |
| 1 000 000 | 𓁨 | Heh-jumala |
Kun symboleja yhdistettiin ryhmiin, saatiin lukuja. Jos kirjuri halusi kirjoittaa luvun 2324, hän piirsi kaksi lootuskukkaa (2 x 1 000), kolme köyttä (3 x 100), kaksi käänteistä u-kirjainta (2 x 10) ja neljä suoraa viivaa (4 x 1). Tätä voi soveltaa kaikkiin lukuihin, esim. 46 237:
- neljä osoittavaa sormea (4 × 10 000)
- kuusi lootuskukkaa (6 × 1 000)
- kaksi köyttä (2 × 100)
- kolme käänteistä u-kirjainta (3 × 10)
- seitsemän viivaa (7 × 1)
Additiivinen merkintä vaikuttaa jälkiviisaana työläältä – ja sitä se olikin. Suurten lukujen kohdalla sama symboli saattoi toistua kymmeniä kertoja, mikä teki kirjoittamisesta hidasta ja virheherkkää. Luku 999 999 vaatii egyptiläisillä hieroglyfeillä 54 merkkiä, kun nykyisessä järjestelmässä selviää kuudella!
Toisaalta järjestelmä oli aikalaisten näkökulmasta selkeä ja johdonmukainen. Meille hieroglyfit voivat tuntua sekavilta, mutta se johtuu vain vieraista symboleista. Jos muinaisille egyptiläisille näytettäisiin nykyisin käytettävät arabialaiset numerot 0–9, reaktio olisi varmasti sama.
Rhindin papyrus
Nykyinen tietämys egyptiläisten matemaattisista taidoista perustuu yksittäisiin säilyneisiin dokumentteihin. Niistä merkittävin on ns. Rhindin tai Ahmesin papyrus, joka on peräisin noin vuodelta 1650 tai 1550 eaa.
Papuryksen toinen nimi viittaa skotlantilaiseen antikvaariin Henry Rhindiin, joka hankki papyruksen Egyptin Luxorista vuonna 1858. Ahmes taas oli kirjuri, joka kopioi tekstin aiemmasta, sittemmin kadonneesta tekstistä.
Brittiläisessä museossa majaileva papyruskäärö sisältää 84 matemaattista probleemaa. Mukana on myös ratkaisut, mutta ajalle tyypilliseen tapaan kaikkien kohdalla ei kerrota, miten ratkaisuun on päästy. Ongelmat kuvastavat hyvin matematiikan käytännönläheistä luonnetta:
- Miten jakaa leipä tai olut tasaisesti työntekijöille?
- Miten laskea alueen pinta-ala?
- Miten laskea viljasiilon tilavuus?
Yksi tehtävistä kysyy, kuinka 7 leipää jaetaan tasan 10 miehen kesken. Egyptiläiset ratkaisivat tämän käyttämällä yksikkömurtolukuja: jokainen saa 7/10 osan leivästä, joka ilmaistiin murto-osien summana 1/2 + 1/5.
Toisessa tehtävässä lasketaan ympyrän pinta-ala, kun halkaisija on 9 yksikköä. Egyptiläisellä menetelmällä halkaisijasta otetaan 8/9 (eli 9 – 1 = 8) ja tulos korotetaan neliöön (64). Tämä antaa yllättävän tarkan likiarvon ympyrän pinta-alalle ja vastaavan likiarvon π:lle (noin 3,16).
Murtoluvut ja Horuksen silmä
Rhindin papyruksen esimerkit paljastavat, että muinaisilla egyptiläisillä oli oma tapansa käsitellä murtolukuja. Sen sijaan, että murtoluvut olisi kirjoitettu muodossa 2/5, ne ilmaistiin yksikkömurtolukujen (esim. 1/2 tai 1/3) summana: 2/5 = 1/3 + 1/15
Ainoa poikkeus tästä oli murtoluku 2/3, jolle oli oma kirjoitusmerkkinsä. Tämä tuntuu nykyvinkkelistä mutkikkaalta, mutta se sopi hyvin egyptiläisten menetelmiin. Papyruksessa on taulukoita, jotka osoittavat, miten murtolukuja voi muuttaa yksikkömurtolukujen summiksi:
- 2/3 = 1/2 + 1/6
- 2/15 = 1/10 + 1/30
- 2/55 = 1/30 + 1/330
- 2/95 = 1/60 + 1/380 + 1/570
Murtoluvut eivät olleet vain numeroita, vaan niillä oli myös symbolista arvoa. Legendan mukaan Horus-jumalan silmä vaurioitui taistelussa setäänsä Sethiä vastaan, mutta Thot onnistui kokoamaan silmän palaset takaisin yhdeksi. Näin silmästä tuli kokonainen, eheä ja korjattu.
Legendan kunniaksi Horuksen silmä – muinaisegyptiläinen suojeluksen, kuninkaallisen vallan ja terveyden symboli – jaettiin osiin, jotka edustavat murtolukuja:
- silmän oikea puoli = 1/2
- pupilli = 1/4
- kulmakarva = 1/8
- vasen puoli = 1/16
- kaareva häntä = 1/32
- kyynel = 1/64
Kun murtoluvut lasketaan yhteen, tulos osuu lähelle 1:tä. Tämä symboloi Horuksen silmän tavoin kokonaisuutta ja jumalallista järjestystä. Matematiikan symboliikkaa löytyy myös muista muinaisista sivilisaatioista, kuten Kiinasta.
Geometria ja 3–4–5-kolmio
Muinais-Egyptissä geometriaa käytettiin käytännön tarpeesta mitata maata ja rakentaa monumentteja. Rhindin papyrus sisältää kaavoja mm. suorakulmioiden, kolmioiden ja puolisuunnikkaiden pinta-aloille sekä sylinterien ja pyramidien tilavuuksille.
Yksi tunnetuimmista esimerkeistä on egyptiläinen kolmio, joka tunnetaan nykyisin 3–4–5-kolmiona. Egyptiläiset sitoivat naruun 12 solmua tasaisin välein. Kun naru asetettiin kolmion muotoon, sen sivujen pituudet olivat 3, 4 ja 5 solmua, mistä syntyi täydellinen suorakulma.
Oivallus oli ratkaisevassa roolissa temppelien, pyramidien ja kaupunkien rakentamisessa. Se osoittaa myös, että egyptiläisillä oli käytännön ymmärrys Pythagoraan lauseesta vuosisatoja ennen Pythagorasta, joka muotoili sen matemaattiseksi todistukseksi.
Matemaattiset suhteet
Matematiikan historian kontekstissa on tärkeää suhteuttaa egyptiläisten ymmärrys ja saavutukset aikaisempiin, aikalaisiin ja myöhempiin käytäntöihin:
- Babylonialaiset (n. 1900–539 eaa.) kehittivät paikkajärjestelmän, joka mahdollisti suurten lukujen ja murtolukujen käsittelyn huomattavasti tehokkaammin. He osasivat ratkaista toisen asteen yhtälöitä ja tehdä tarkkoja tähtitieteellisiä laskelmia.
- Egyptiläiset (n. 3150–30 eaa.) sovelsivat geometriaa ja ratkaisivat käytännön ongelmia, mutta heidän matematiikkansa oli vähemmän abstraktia, eikä merkintätapa ei ollut yhtä joustava kuin babylonialaisten.
- Kreikkalaiset (n. 800 eaa.–300 jaa.) perivät egyptiläisten käytännön menetelmät ja babylonialaisen teorian. He rakensivat niistä deduktiivisen järjestelmän, jossa ei tyydytty tulosten laskemiseen vaan kaikki johdettiin peruskäsitteistä eli aksiomeista.
Egyptiläisen matematiikan ydin oli siis käytännöllisyydessä. He loivat järjestelmän, joka vastasi sekä arkisia että hallinnollisia tarpeita, mutta käytännöllisyys toi mukanaan rajoituksensa: menetelmät olivat tuloksineen usein likimääräisiä, eivät täsmällisiä.
Matematiikan kehitys vaikuttaa hidastuneen Rhindin papyruksen jälkeen. Koska huomio kohdistui käytännön ongelmiin, egyptiläiset eivät (tiettävästi) edenneet abstraktien teorioiden kehittämiseen. Järjestelmä loi joka tapauksessa pohjaa myöhemmille sivilisaatioille ja toimii muistutuksena siitä, että innovaatio syntyy usein käytännön tarpeesta.
Piditkö tästä artikkelista? Jätä arvostelu!
Ladataan...
