Kiina tunnetaan nykyään maailman suurimpana tuotantokeskuksena, mutta jos matkaamme tuhansia vuosia ajassa taaksepäin, kohtaamme toisenlaisen maailman: kilpailevia dynastioita, oraakkeliluita ja esi-isien palvontaa.
Varhaisimmat kiinalaiset numeromerkit löytyvät Shang-dynastian (n. 1600–1046 eaa.) oraakkeliluista – kilpikonnan kuorista ja uhrieläinten lapaluista, joihin kaiverrettiin kysymyksiä ja merkkejä, myös numeroita. Kun luut kuumennettiin, niihin syntyi halkeamia, jotka tulkittiin esi-isien viesteiksi.
Numeroilla oli uskonnossa sekä käytännöllinen että rituaalinen merkitys. Niiden avulla kirjattiin seremonioita, merkittiin muistiin ennusteita ja laskettiin uhrattuja eläimiä. Numerot ovatkin olleet osa Kiinan poliittista, uskonnollista ja sosiaalista rakennetta vuosituhansien ajan.
Mihin matematiikkaa tarvittiin?
Muinainen Kiina ei ollut aina yhtenäinen valtakunta. Taistelevien läänitysvaltioiden kaudella (475–221 eaa.) vallasta kamppaili seitsemän valtiota, ja yhteiskuntaa leimasivat jatkuva sota, vaihtuvat liittolaiset sekä hallinnollinen kilpavarustelu. Sotaisassa yhteiskunnassa oli monia hallinnollisia tarpeita, joita täytettiin matematiikan avulla:
- Maatalous ja verotus. Keltaisenjoen laakso oli koti miljoonille maanviljelijöille, joiden maapalstat tuli mitata ja verottaa. Virkamiehet laskivat satoja, veroja ja varastointitarpeita.
- Hallinto ja väestönlaskenta. Dynastiat pitivät tarkkaa kirjaa kotitalouksista, työntekijöistä, sotilaista ja tarvikkeista. Byrokratian ratas ei pyörinyt ilman matematiikkaa.
- Sotilaslogistiikka. Sodat olivat valtavia operaatioita, joissa liikkui tuhansia sotilaita. Armeijoiden ruokkiminen, aseistaminen ja liikutteleminen olivat pohjimmiltaan matemaattisia ongelmia.
- Insinööritaidot ja rakentaminen. Valtiot investoivat myös rauhan infrastruktuuriin, kuten kastelukanaviin, teihin ja muureihin. Niiden rakentaminen edellytti laskelmia pinta-aloista, tilavuuksista ja materiaaleista.
Kiinan kohdalla pitää korostaa myös tähtitieteen ja kalenterin roolia, sillä poliittinen valta nojasi ajatukseen taivaan mandaatista. Hallitsijan uskottiin ylläpitävän harmoniaa maan ja taivaan välillä, mikä teki kalenterin laatimisesta keskeisen matemaattisen tehtävän.
Oikea-aikainen kylvö, sadonkorjuu ja juhlapäivät vahvistivat hallitsijan asemaa, kun taas virheellinen kalenteri saattoi horjuttaa koko dynastian legitimiteettiä. Matematiikka olikin kiinteä osa valtioiden ja kiinalaisen yhteiskunnan tarpeita. Käytännöllinen lähestymistapa näkyy myös muissa muinaisissa laskujärjestelmissä.
Kiinalainen numerojärjestelmä
Kiinalaiset kehittivät loogisen ja johdonmukaisen desimaalijärjestelmän tuhansia vuosia sitten, kauan ennen nollan tai paikkaluvun keksimistä. Desimaali- eli kymmenjärjestelmän kantalukuna on 10: kymmenessä on kymmenen ykköstä (101), sadassa kymmenen kymmentä (102), tuhannessa kymmenen sataa (103) jne.
Järjestelmässä käytettiin numeroita 1–9:
| Luku | Merkki |
|---|---|
| 1 | 一 (yī) |
| 2 | 二 (èr) |
| 3 | 三 (sān) |
| 4 | 四 (sì) |
| 5 | 五 (wǔ) |
| 6 | 六 (liù) |
| 7 | 七 (qī) |
| 8 | 八 (bā) |
| 9 | 九 (jiǔ) |
Näiden lisäksi jokaisella kymmenen potenssilla oli oma merkkinsä:
- 十 (shí) = 10
- 百 (bǎi) = 100
- 千 (qiān) = 1 000
- 万 (wàn) = 10 000
- 亿 (yì) = 100 000 000
Numerot muodostettiin kahden yksinkertaisen säännön avulla:
Pienempi luku suuremman jäljessä = yhteenlasku
- 百三 = 100 + 3 = 103
- 百十三 = 100 + 10 + 3 = 113
Pienempi luku suuremman edellä = kertolasku
- 三百 = 3 × 100 = 300
- 三十三 = 3 × 10 + 3 = 33
Koska järjestelmä ei ollut paikkajärjestelmä, nollaa ei tarvittu. Luvun arvo ei siis riippunut käytettävien numeromerkkien keskinäisestä järjestyksestä. Luku 1030 kirjoitettiin muodossa 一千三十 ("tuhat kolmekymmentä"), eikä puuttuville sadoille tarvittu erillistä merkkiä.
Järjestelmän toinen erityinen piirre liittyi suurten lukujen ryhmittelyyn. Länsimaissa järjestelmissä numerot jaotellaan tuhansittain: 1 000 (10³), 1 000 000 (10⁶), 1 000 000 000 (10⁹). Kiinassa ryhmittely tehtiin kymmentuhansittain:
- 万 (wàn) = 10 000 (10⁴)
- 亿 (yì) = 100 000 000 (10⁸)
Tämä tarkoitti sitä, että 10 000 ei ollut vain "kymmenentuhatta" vaan laskennan perusyksikkö: 120 000 = 12 wàn (万). Ryhmittely näkyy nykyisessä järjestelmässä yhä, sillä kiinalaiset talousraportit ja uutiset esittävät luvut yleensä kymmenissä tuhansissa tai sadoissa miljoonissa.
Jos tämä artikkeli jättää nälkäiseksi, voit seuraavaksi sukeltaa antiikin Egyptin numeroihin!
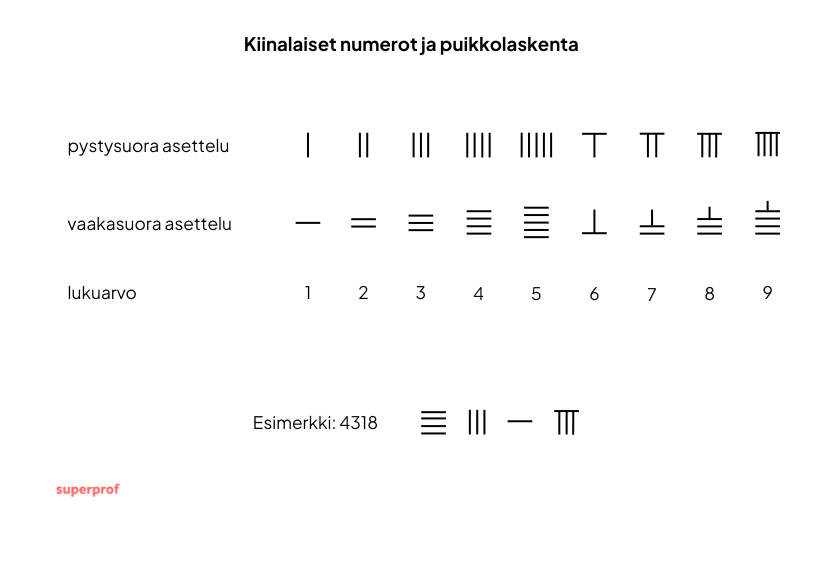
Laskentapuikot ja matemaattiset tekstit
Kirjoitettu numeromerkistö palveli hallintoa ja kirjallisuutta, mutta käytännön laskenta hoidettiin laskentapuikoilla (suànchóu). Ne olivat 12–15 cm pitkiä bambu- tai luutikkuja, joita aseteltiin laskentapöydälle.
- Luvut 1–4 merkittiin pystypuikoilla (|, ||, |||, ||||).
- Luku 5 merkittiin vaakapuikolla (—).
- Luvut 6–9 muodostettiin vaakapuikon ja pystypuikkojen yhdistelmillä (—| = 6, —|| = 7, … —|||| = 9)
Paikkajärjestelmä toteutettiin asettamalla puikot laskentapöydän eri sarakkeisiin (ykköset, kymmenet, sadat, tuhannet). Jotta sarakkeiden numerot eivät sekoittuisi keskenään, ykköset ja sadat merkittiin pystypuikoilla, kymmenet ja tuhannet vaakapuikoilla.
Alun perin järjestelmässä ei ollut nollan merkkiä, vaan se korvattiin tyhjällä sarakkeella. Myöhemmin nolla sai oman symbolinsa (〇 tai 零), mutta ajatus "ei mistään" oli olemassa jo kauan ennen tätä. Puikkojen avulla kiinalaiset matemaatikot pystyivät laskemaan muun muassa
- suuria kerto- ja jakolaskuja
- murtolukuja ja verrannollisuutta
- negatiivisia lukuja (puikon värin tai suunnan avulla)
- neliöjuuria.
Puikkojärjestelmä oli joustava työkalu, jota hyödynsivät niin kauppiaat, verottajat kuin tähtitieteilijät. Käytännön rinnalle syntyi myös kirjallista matematiikkaperinnettä, josta muutama tunnetaan tänä päivänä:
Zhoubi Suanjing (n. 500–200 eaa.) yhdisti tähtitiedettä, geometriaa ja rituaaleja. Teoksessa on suorakulmaiseen kolmioon liittyviä ongelmia, jotka muistuttavat Pythagoraan lausetta.
Suàn shù shū (n. 200 eaa.) sisälsi 200 ongelmaa verotuksesta, ruoan jakelusta ja geometriasta. Teksti löydettiin Han-dynastian aikaisesta haudasta.
Jiǔ zhāng Suàn shù ("Yhdeksän lukua matematiikan taidosta", n. 200 eaa.) nousi kiinalaisen matematiikan klassikoksi. Se käsittelee kaikkea pinta-aloista ja tilavuuksista matriiseihin ja muodosti olennaisen osan virkamiesten koulutuksesta.
Yhdeksän lukua painotti käytännön ratkaisuja, mikä kuvasti aikakauden matematiikkaa laajemminkin. Myöhemmin antiikin Kreikassa keskiöön nousivat deduktiivinen menetelmä, todistukset ja matematiikan teoreettinen tarkastelu.
Perintö ja kulttuurinen merkitys
Kiinalaisen matematiikan perintö näkyy sekä käytännössä että kulttuurissa. Käytännön puolella desimaalijärjestelmä oli vuosisatoja edellä eurooppalaista vastinettaan, ja puikkolaskenta näytti suuntaa helmitaululle, jota käytetiin apuvälineenä 1900-luvun lopulle asti.
Muinaiset kiinalaiset numerot ovat myös monin paikoin edelleen käytössä. Yksinkertaistetut merkit 1, 2, 3 ja 8 (一，二，三，八) ovat pysyneet samoina tuhansien vuosien. Toiset, kuten viisi ja kymmenen (五，十), heijastavat puolestaan laskutikkuperinnettä.
Kulttuurin osalta tietyillä numeroilla on ollut pitkään symbolinen merkitys:
- 4 (sì) kuulostaa samalta kuin kuolemaa tarkoittava sǐ, ja sitä vältetään sairaaloiden, hotellien ja huoneistojen numeroissa. Muistuttaa länsimaiden numeroa 13.
- 6 (liù) kuulostaa samalta kuin virtausta tarkoittava liú, minkä ajatellaan tuovan onnea liiketoimintaan. Siksi hinnat ja tarjoukset päättyvät usein numeroon 6.
- 8 (bā) kuulostaa samalta kuin vaurautta tarkoittava fā, ja sitä pidetään onnen numerona. Puhelinnumerot, rekisterikilvet ja osoitteet, joissa on numero 8, ovat kovaa valuuttaa.
- 9 (jiǔ) kuulostaa samalta kuin ikuisuutta tarkoittava jiǔ. Sitä pidetään keisarillisena numerona, joka näkyy Kielletyn kaupungin Palatsimuseon 9 999 huoneessa.
Kiinalainen numerojärjestelmä osoittaa, ettei matematiikka ollut vain laskemista vaan myös kulttuuria, hallintoa ja uskontoa. Bambupuikot, desimaalijärjestelmä ja matemaattiset klassikot loivat raamit, joita hyödynnettiin niin viljan laskussa kuin palatsien rakentamisessa. Samalla numerot saivat symbolisia merkityksiä, jotka näkyvät kiinalaisessa arjessa yhä.
Kun tätä verrataan Babylonian paikkajärjestelmään, Egyptin yksikkömurtoluikuihin tai Kreikan todistusperinteeseen, on selvää, että jokainen korkeakulttuuri toi matematiikkaan oman säväyksensä. Yhdessä nämä perinteet loivat rikkaan ja monimuotoisen pohjan, jolle moderni matematiikka rakentuu.
Piditkö tästä artikkelista? Jätä arvostelu!
Ladataan...
