Antiikin sivilisaatioista muistetaan erityisesti Egypti – kenties siksi, että sen pyramidit seisovat yhä tai koska suomalaiset ovat matkanneet sinne Sinuhen siivillä. Niilin laakson itäpuolella, Eufratin ja Tigrisin välimaastossa, kukoisti kuitenkin toinen kulttuuri, jonka vaikutus matematiikan kehitykseen oli vähintään yhtä merkittävä: Babylonia.
Kauan ennen Pythagorasta ja kumppaneita babylonialaiset ratkaisivat toisen asteen yhtälöitä, laativat monimutkaisia lukutaulukoita ja kehittivät laskujärjestelmän, jonka jäljet näkyvät arjessamme yhä. Tämä artikkeli esittelee babylonialaisen matematiikan historiaa, numerojärjestelmää, menetelmiä ja perintöä.
Babylonialainen matematiikka
Babylonia sijaitsi muinaisessa Mesopotamiassa (Kaksoisvirranmaassa) Välimeren itäpuolella, nykyisen Irakin, Syyrian ja Turkin alueilla. Nimensä se sai kreikan sanoista meso ("välissä") ja potamoi ("virrat"), jotka viittaavat alueen halki virtaaviin Eufratiin ja Tigrisiin.
Mesopotamia tunnetaan sivistyksen kehtona, jossa kehitettiin muun muassa maanviljely, kaupungit ja kirjoitustaito. Se ei ollut kuitenkaan yksi valtakunta, vaan kehitystä tapahtui tuhansien vuosien aikana eri kansojen alaisuudessa, kuten sumerien, akkadilaisten ja myöhemmin babylonialaisten.
Babylonia kasvoi suurvallaksi noin 1750 eaa. kuningas Hammurabin johdolla. Valtakunnan matematiikka kehittyi käytännön tarpeisiin, kuten peltojen mittaamiseen, vilja-annosten laskemiseen, verotukseen ja temppeleiden rakentamiseen.
Nuolenpääkirjoituksen taitaneet kirjurit saivat vuosien koulutuksen, ja heitä tarvittiin kaikkialla: temppeleissä, hallinnossa, kaupankäynnissä. Matematiikka ei ollut jokamiehen taito, mutta se oli yhteiskunnan toiminnan kannalta välttämätön.
Babylonialaiset numerot
Ennen babylonialaisia numeroita on hyvä palauttaa mieleen, miten oma järjestelmämme toimii. Nykyisessä paikkajärjestelmässä numeron merkitys riippuu sen paikasta: luvussa 1234 on vasemmalta oikealle tuhannet (1000), sadat (200), kymmenet (30) ja ykköset (4).
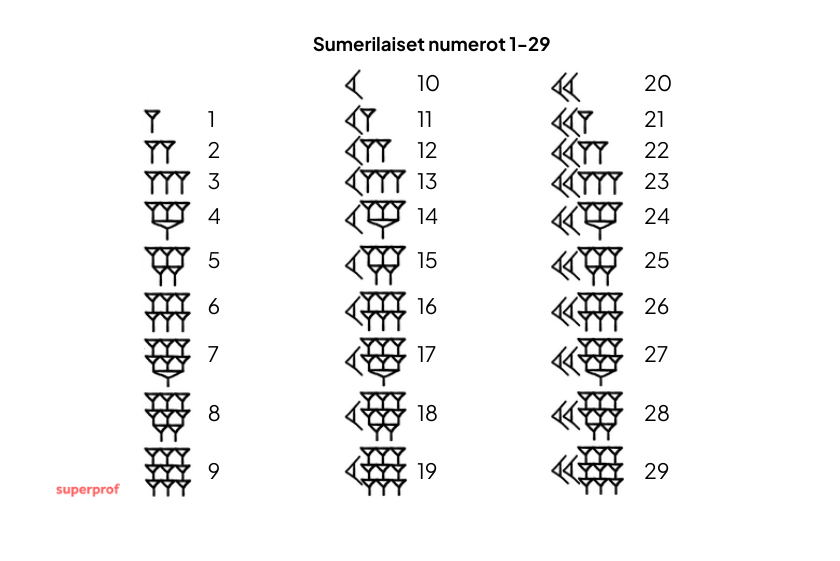
Ennen kuin babylonialaiset loivat vastaavanlaisen menetelmän, käytössä oli sumerien kehittämä yksinkertainen nuolenpääkirjoitus: yksi pystysuora kiila merkitsi ykköstä, kaksi kiilaa kahta, kolme kiilaa kolmea ja niin edelleen.
Numerot eivät olleet sidoksissa paikkaan, mitä voi verrata roomalaisiin numeroihin: kympin symboli X tarkoitti aina kymppiä, olipa se luvussa XX (20) tai CX (110). Järjestelmä toimi, mutta suurten lukujen kirjoittaminen oli kömpelöä ja laskeminen hidasta.
Läpimurto tapahtui noin 2000 eaa., kun babylonialaiset muovasivat ykkösistä ja kympeistä paikkajärjestelmän. Siinä numeron arvo riippuu sen sijainnista – aivan kuten meille tutussa desimaalijärjestelmässä. Ainoa ero oli se, että kantalukuna oli 10:n sijaan 60. Esimerkiksi luku 73 kirjoitettiin muodossa 1,13: yksi 60 ja kolmetoista ykköstä.
Babylonialaisessa järjestelmässä ei ollut varsinaista nollamerkkiä tai pilkkua, vaan lukujen paikat erotettiin alun perin tyhjällä kohdalla – hieman kuin välilyönti luvussa 1 000. Nykytutkimuksessa käytetty pilkku (esim. 1,13) ei ole desimaalipilkku vaan apumerkki paikan erottamiseen.
Miksi juuri 60? Koska se on jaollinen monella eri luvulla (1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60), mikä helpottaa laskemista. Jos olet joskus miettinyt, miksi minuutissa on 60 sekuntia tai ympyrässä 360 astetta, vastaus löytyy Babyloniasta.
Jos haluat tutustua myös muihin vanhoihin laskenta- ja numerojärjestelmiin, kiinalaisten puikkolaskenta on parhaasta päästä!
Sukellus seksagesimaalijärjestelmään
Babylonialaisten kehittämää järjestelmää kutsutaan seksagesimaalijärjestelmäksi (lat. sexagesimus = kuudeskymmenes). Numerot kirjoitettiin puukiiloilla savitauluihin, ja käytössä oli kaksi perusmerkkiä: pystysuora kiila (𒁹) vastasi ykköstä ja kulmakiila (𒌋) kymppiä. Niitä yhdistämällä saatiin luvut 1–59.
Koska kyseessä oli paikkajärjestelmä, merkin arvo riippui sen sijainnista. Oikealta katsottuna ensin tulivat ykköset (60⁰), sitten 60:t (60¹), sen jälkeen 3600:t (60²) ja niin edelleen:
- 1,13 = 1 x 60 + 13 = 73
- 1,40 = 1 x 60 + 40 = 100
(Huom. pilkku on moderni apumerkki paikkojen erottamiseen, ei babylonialaisten oma käytäntö!)
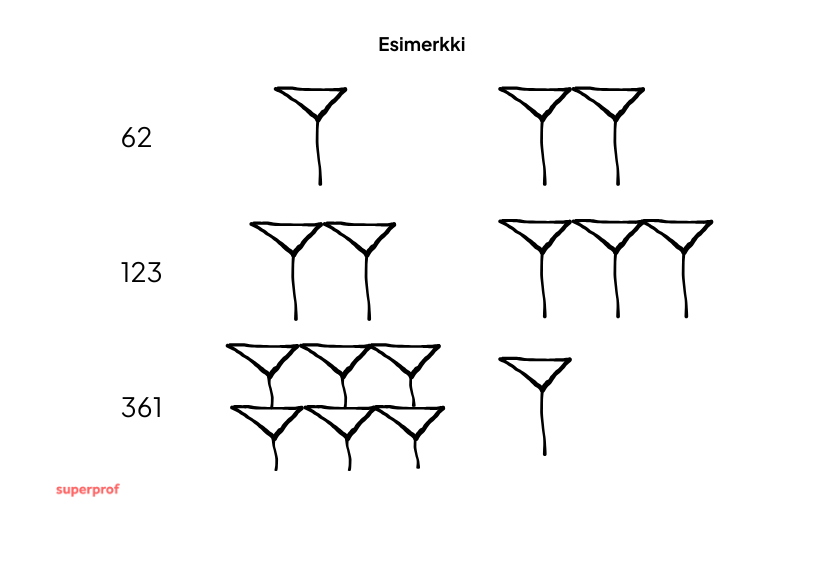
Entäpä suuremmat luvut? Tässä luku 3754, joka merkitään 60-järjestelmässä 1,2,34:
Kymmenjärjestelmä
- 3000 (3 x 103)
- 700 (7 x 102)
- 50 (5 x 101)
- 4 (4 x 100)
60-järjestelmä
- 1 (1 x 602 = 3600)
- 2 (2 x 601 = 120)
- 34 (34 x 600 = 34)
Samaa menetelmää voi soveltaa myös murtolukuihin:
- 1/2 = 0,30 (30/60)
- 1/3 = 0,20 (20/60)
Kantaluku 60 voi vaikuttaa aluksi hankalalta, mutta se teki monista jakolaskuista yllättävän käteviä! Järjestelmällä oli kuitenkin rajoituksensa. Ilman selkeää nollaa tai desimaalipilkkua yksiköiden paikat piti päätellä kontekstista. Sama merkintä 𒌋𒌋𒁹𒁹𒁹 saattoi tarkoittaa:
- 23 (23 × 60⁰; 𒌋𒌋𒁹𒁹𒁹)
- 23 × 60 (23 × 60¹; 𒌋𒌋𒁹𒁹𒁹␣)
- 23 × 3600 (23 × 60²; 𒌋𒌋𒁹𒁹𒁹␣␣)
Matematiikkaa savitauluilla
Babylonialaiset kirjasivat laskelmansa märkiin savitauluihin, jotka kuivatettiin tai kovetettiin polttamalla. Toisin kuin Egyptin hauraat papyrusrullat, taulut säilyivät tuhansia vuosia ja antavat tutkijoille valtavasti tietoa ajan kulttuurista.
Vanhan Babylonian kaudelta (n. 1830–1530 eaa.) tunnetaan noin 400 matemaattista taulua, joita on löydetty muun muassa Urukin ja Larsan alueilta. Nykyään niitä säilytetään museoissa ympäri maailmaa, ja tutkijat ovat sittemmin oppineet lukemaan niiden kiilakirjoitusta.
Taulut sisältävät kaikkea algebrallisista ongelmista ja geometrisista laskelmista neliö- ja käänteislukutauluihin. Taulut olivat lähes poikkeuksetta käytännöllisiä ja ratkoivat arjen kysymyksiä:
- Kuinka paljon viljaa maanviljelijä saa?
- Kuinka maa jaetaan tasan perillisten kesken?
- Kuinka rakentaa temppeli tarkkojen mittasuhteiden mukaan?
Babylonialainen järjestelmä taipui kuitenkin myös laskuihin, joita pidetään edelleen "edistyneinä": murtolukuihin, käänteislukuihin ja neliöjuuriin – ilman moderneja työkaluja. Koska laskut saattoivat viedä aikaa, apuna käytettiin valmiita taulukoita..
Yhteen tauluun saatettiin kirjata lukujen 1–60 neliöt, jotta vastausta ei tarvinnut laskea joka kerta uudelleen. Käänteislukutaulukot (luvut, joiden kertolaskun tulos on 1) helpottivat puolestaan jakolaskuja. Niitä voi verrata koulussa käytettyyn kertotauluun, mutta 60-järjestelmä teki niistä vielä mutkikkaampia.
Babylonialaiset olivatkin systemaattisen laskennan suunnannäyttäjiä. Taulukot helpottivat muistamista, nopeuttivat laskemista ja näyttivät suuntaa tuleville matemaattisille työkaluille.
Pythagoraan kolmikko
Pythagoraan lause ja siihen liittyvä Pythagoraan kolmikko soittavat varmasti kelloja, jos on sattunut opiskelemaan matematiikkaa yläasteella. Kreikkalaisen filosofin mukaan nimetty teoreema kuuluu näin: "Suorakulmaisen kolmion kateettien pituuksien a ja b neliöiden summa on hypotenuusan pituuden c neliö". Toisin sanoen a2 + b2 = c2.
Harvaa tietää, että Pythagoras ei ollut säännön keksijä. Sekä muinaiset egyptiläiset että babylonialaiset hyödynsivät sääntöä yli tuhat vuotta ennen herran syntymää. Egyptissä sääntöä käytettiin temppelien, pyramidien ja kaupunkien rakentamisessa. Babyloniasta on puolestaan kantautunut tarina maanmittaajasta, joka käytti työssään apuna pientä taulua. Taululla oli useita laskelmia, muun muassa 32 + 42 = 52.
Babylonialaisen matematiikan vaikutus ulottuu kauas Mesopotamian rajojen ulkopuolelle. Kreikkalaiset omaksuivat monia sen menetelmiä ja jalostivat niistä edelleen matemaattisia todistuksia ja teorioita. Myös kreikkalainen tähtitiede – Hipparkhos ja myöhemmin Ptolemaios – pohjautui pitkälti babylonialaiseen havaintoperinteeseen ja laskentaan.
Babylonian perintö näkyy meidän kaikkien arjessa:
- minuutissa on 60 sekuntia
- tunnissa 60 minuuttia
- ympyrässä 360 astetta.
Savitaulut korostavat matematiikan käytännöllisyyttä, mutta ne osoittavat myös, että babylonialaiset ottivat ensiaskeleita kohti teoreettista matematiikkaa. Monet laskelmat ratkaisivat rakentamiseen tai kaupankäyntiin liittyviä ongelmia, mutta mukana oli myös laskuja, jotka olivat käytännöstä irrallaan.
Babylonialaiset olivatkin ensimmäisten joukossa tutkimassa matematiikkaa sen itsensä takia. Tämä lienee heidän suurin panoksensa matematiikan kehitykseen: askel kohti abstraktia ajattelua, joka puhkesi antiikin Kreikassa kukkaansa.
Piditkö tästä artikkelista? Jätä arvostelu!
Ladataan...
