Jotkut maailman loistavimmista mielistä seisovat differentiaali- ja integraalilaskennan kehityksen takana ja pitävät sitä yhtenä tärkeimmistä koskaan luoduista matemaattisista tieteenaloista. Laskenta on tarjonnut ihmiskunnalle välineet ymmärtää, kuvata ja ennustaa ilmiöitä maailmassa, joka on jatkuvassa muutoksessa.
Ilman laskentaa eli differentiaali- ja integraalilaskentaa monet nykyteknologiat, luonnontieteelliset läpimurrot ja taloudelliset mallit olisivat mahdottomia. Laskenta voi tuntua alkuun vaikealta, mutta se on äärimmäisen looginen ja käytännöllinen matematiikan osa-alue.
Aikaisemmin muuttuvan maailman ilmiöiden analysointi oli työlästä ja aikaa vievää. Laskennan ansiosta näin ei enää ole. Siitä huolimatta erityisesti opiskelijat eivät koe sitä mielekkääksi. Differentiaali- ja integraalilaskennan opiskelu vaatii systemaattista harjoittelua ja perusasioiden säännöllistä kertaamista.
Tässä artikkelissa tarkastelemme keskeisiä laskennan osa-alueita, yleisiä haasteita ja käytännön vinkkejä, joiden avulla laskentaan liittyviä ongelmia voidaan ymmärtää ja hallita paremmin. Tarkastelemme kaikkea derivoinnista integrointiin mukaan lukien raja-arvojen sekä differentiaaliyhtälöiden periaatteet.

Laskennan periaatteet ja asiaa raja-arvoista
Siitä lähtien, kun Isaac Newton kehitti laskennan perusperiaatteet 1600-luvun lopulla, sitä on käytetty monilla eri aloilla ratkaisemaan muuttuvan maailman haasteita. Differentiaali- ja integraalilaskennan ytimessä on muutos.
Vaikka Isaac Newton kehitti laskennan, nykyään sen keskeisimpien osa-alueiden edistäjänä pidetään Gottfried Leibnizia.
Toisin kuin perinteinen algebra tai geometria, laskenta keskittyy siihen, miten suureet muuttuvat ajan, paikan tai muiden muuttujien funktiona. Tätä varten yksi keskeisimmistä käsitteistä on raja-arvo. Raja-arvo kuvaa arvoa, jota funktio lähestyy, kun muuttuja lähestyy tiettyä pistettä.
Raja-arvot ovat välttämättömiä, jotta voidaan määritellä funktion jatkuvuus, derivaatat ja integraalit. Ilman raja-arvoja laskenta menettäisi teoreettisen perustansa. Raja-arvojen avulla voidaan esimerkiksi tutkia, käyttäytyykö funktio loogisesti tietyn pisteen läheisyydessä, vai esiintyykö esimerkiksi äärettömiä arvoja.

Tässä yksinkertainen esimerkki: Funktiolle, (a)f ( x ) = 8 − x³ x² − 4 f(x)=8 − x³ x² − 4, arvioi seuraavien funktion arvojen funktio xx (vähintään kahdeksan desimaalin tarkkuudella).
- 2.5,
- 2.1,
- 2.01,
- 2.001,
- 2.0001,
- 1.5,
- 1.9,
- 1,99,
- 1.999,
- 1.9999
Käytä kohdan (a) tietoja arvioidaksesi arvonraja lim x → 28 − x 3 x 2 − 4, lim x →28 − x 3 x 2 −.
Käytännön laskennassa raja-arvot auttavat hahmottamaan, miten funktio käyttäytyy ilman, että arvoa tarvitsee laskea täsmälleen kyseisessä pisteessä. Tämä ajattelutapa on keskeinen koko differentiaali- ja integraalilaskennan ymmärtämisessä.
Derivointi ja differentiaalilaskennan keskeiset periaatteet
Derivointi on differentiaalilaskennan ydin. Derivaatta kuvaa funktion muutosnopeutta ja kertoo, kuinka nopeasti funktion arvo muuttuu muuttujan muuttuessa. Yksinkertaisimmillaan derivointi vastaa kysymykseen: kuinka jyrkkä käyrä on tietyssä pisteessä?
Derivaattoja hyödynnetään monilla eri aloilla. Fysiikassa derivaatta voi kuvata nopeutta tai kiihtyvyyttä, taloustieteessä kustannusten tai tuottojen muutosta ja biologiassa populaation kasvunopeutta. Derivoinnin avulla voidaan löytää maksimi- ja minimiarvoja, optimoida prosesseja ja ennustaa tulevaa.
Derivointisäännöt ja sovellukset
Derivoinnin hallinta edellyttää useiden perussääntöjen ymmärtämistä. Näitä ovat muun muassa summasääntö, tulosääntö, osamääräsääntö ja ketjusääntö. Lisäksi trigonometristen, eksponentiaalisten ja logaritmifunktioiden derivaatat muodostavat keskeisen osan differentiaalilaskentaa.
Alkuvaiheessa derivointitehtävät voivat tuntua monimutkaisilta, mutta säännöllinen harjoittelu tekee niistä nopeasti rutiininomaisia. Tärkeintä on ymmärtää, mitä derivaatta tarkoittaa käytännössä, eikä vain opetella kaavoja ulkoa.
Koska pidämme kuitenkin esimerkeistä, alla joitakin derivaattojen peruskaavoja, joiden avulla opimme, miten derivaattojen määritelmän tunteminen voi auttaa ongelman ratkaisemisessa ja miten funktion derivaatta lasketaan:
- f ( x ) = 6 f(x)=6
- V ( t ) = 3 − 14t , jossa V(t)=3 − 14t
- g ( x ) = x² g (x)=
Derivointi ei ole irrallinen taito, vaan se toimii perustana muun muassa differentiaaliyhtälöille.

Integraalilaskenta ja kokonaisuuksien hahmottaminen
Siinä missä derivointi tarkastelee muutoksen nopeutta, integraalilaskenta keskittyy kokonaisuuksiin. Integroiminen auttaa vastaamaan kysymykseen: kuinka paljon jotakin kertyy ajan tai muun muuttujan kuluessa? Sitä käytetään muun muassa pinta-alojen, tilavuuksien, massojen ja kokonaisenergian laskemiseen.
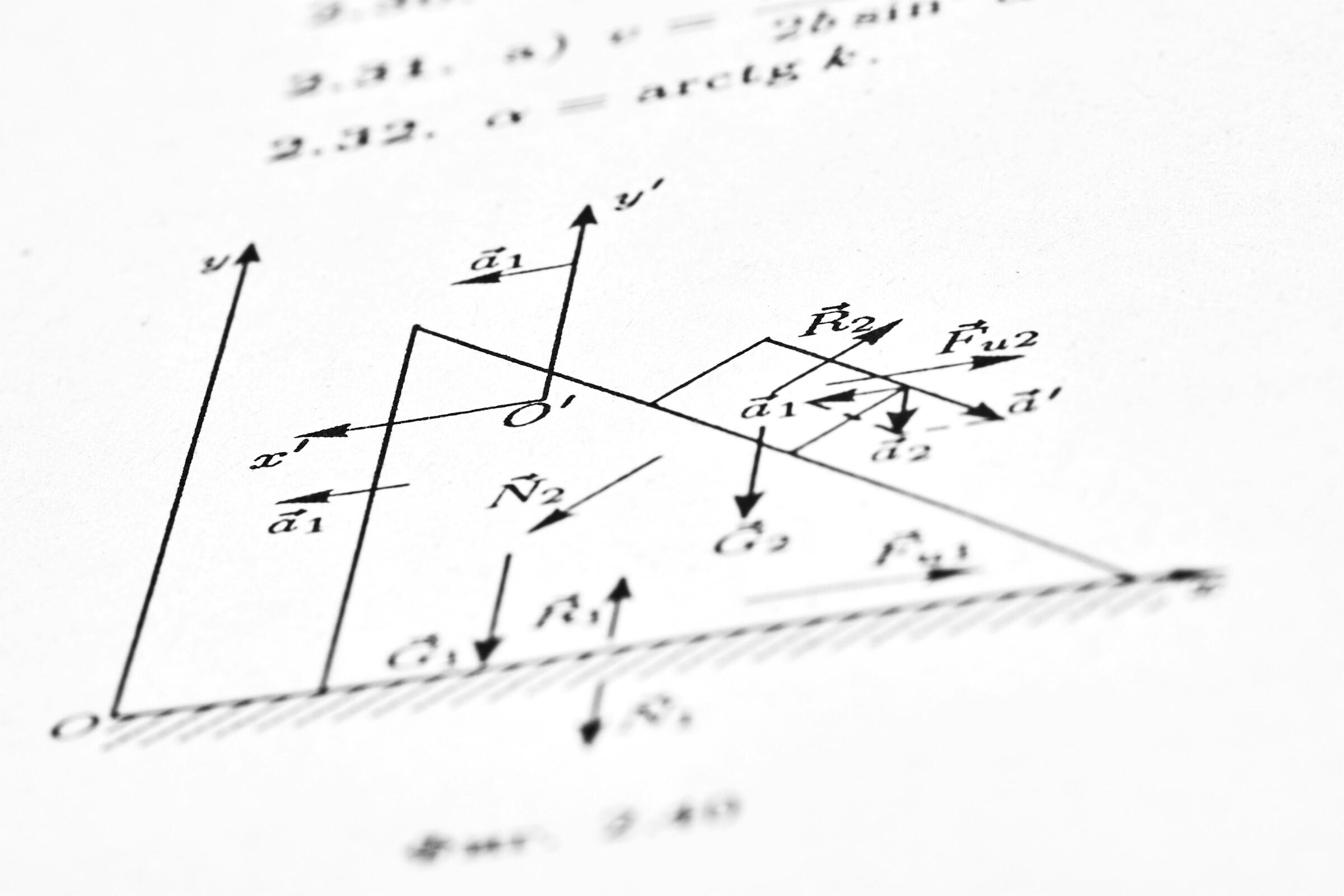
Keskeisiä käsitteitä ovat määräämättömät ja määrätyt integraalit sekä integraalin laskusäännöt. Integraalilaskennan ymmärtämisessä auttaa ajatus funktion kuvaajan alle jäävästä pinta-alasta. Käytännössä integraali voidaan ajatella luonnollisena vastakohtana derivoinnille.
Alla on joitakin integraalilaskennan ongelmia, joihin opiskelijat saattavat törmätä kertaillessaan määräämättömiä integraaleja:
- ∫ 6 × 5 − 18 × 2 + 7d x ∫6x5−18x2+7dx
- ∫ 6 x 5dx − 18x²+ 7 ∫6x5dx −18x²+7
Differentiaali- ja integraalilaskenta liittyvät toisiinsa läheisesti niin sanotun analyysin peruslauseen kautta, joka osoittaa, että derivointi ja integrointi ovat toistensa käänteisoperaatioita.
Differentiaaliyhtälö ja laskennan soveltaminen todelliseen maailmaan
Differentiaaliyhtälö on yhtälö, jossa esiintyy yhden tai useamman muuttujan funktio ja sen derivaattoja. Differentiaaliyhtälöt ovat keskeinen työkalu, kun halutaan mallintaa todellisia ilmiöitä, joissa muutos riippuu nykytilasta.
Esimerkiksi fysiikassa liikelait, lääketieteessä lääkeaineen pitoisuus kehossa ja taloustieteessä investointien kasvu voidaan kuvata differentiaaliyhtälöiden avulla. Differentiaaliyhtälöiden ratkaiseminen edellyttää hyvää derivoinnin ja integraalilaskennan hallintaa.
Differentiaaliyhtälöitä on monenlaisia. On tavallisia differentiaaliyhtälöitä ja osittaisdifferentiaaliyhtälöitä. Ne voidaan myös jakaa joko lineaarisiin ja epälineaarisiin. Vaikka aihe on vaativa, se avaa ovia moniin käytännön sovelluksiin työelämässä ja jatko-opintoihin uran alkuvaiheessa.
Käytännön vinkkejä laskennan oppimiseen
Siitä huolimatta millä tasolla olet tällä hetkellä differentiaali- ja integraalilaskennan parissa, aina löytyy uutta opittavaa ja kehitettävää. Lisäksi mitä tehokkaammin saat luotua laskennan perusteista automaatioita, sitä helpompi sinun on lähteä soveltamaan sitä edistyneellä tasolla.
Maailman parhaimmatkin matemaatikot oppivat jatkuvasti lisää ja löytävät keinoja laskennan soveltamiseen uusien ongelmien ratkaisemiseen. Opiskeluvaiheessa tämä ajatus tulevaisuuden innovaatioista saattaa olla hyvinkin motivoivaa.

Mutta mitkä ovat sitten parhaat vinkit tehokkaaseen laskennan opiskeluun? Kiitos internetin ihmeellisen maailman, joka kulman takaa löytyy jonkun vinkki, mielipide ja materiaali opiskeluun - mutta mitkä näistä oikeasti ovat toimivia? Opiskelussa monesti vanhat tutut vinkit toimivat parhaiten.
Ja jos olet jo hankkinut matematiikan yksityisopettajan, voi yksilöllisiä vinkkejä kysyä suoraan opettajalta. Tämä onkin yksi opetukseen osallistumisen hyvistä puolista, sillä apua ja tukea saa samalla myös itsenäisen opiskelun suunnitteluun.
Vaikka laskenta voi tuntua haastavalta, oikeilla opiskelutavoilla se on täysin hallittavissa. Tärkeimpiä vinkkejä ovat:
Differentiaali- ja integraalilaskenta ovat keskeisiä matematiikan osa-alueita, jotka auttavat ymmärtämään ja mallintamaan muuttuvaa maailmaa. Raja-arvot, derivointi, integraalit ja differentiaaliyhtälöt ovat osa laskennan perusteita.
Oikealla asenteella, säännöllisellä harjoittelulla ja toimivilla opiskelumenetelmillä laskennasta voi tulla jopa oma suosikkisi kaikista matematiikan osa-alueista. Ja kun vihdoin ymmärrät sen käytännön merkityksen oikeassa elämässä, ei teoriankaan opiskelu tunnu niin pahalta!
Tiivistä tekoälyn avulla:















